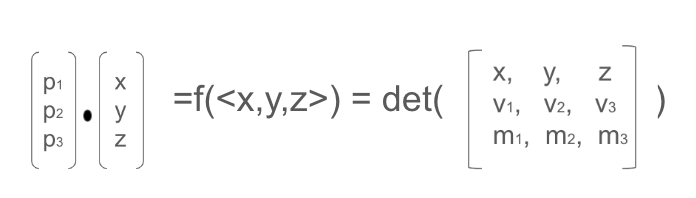Vectors

Vectors are the foundational building blocks of linear algebra. I used to find them abstract and difficult to grasp, which is why this blog is dedicated to cultivating an intuitive understanding of vectors.

Vectors can be interpreted in various ways—mathematically, computationally, and physically. Let’s begin with the mathematical interpretation. In a two-dimensional space, we typically represent a vector v as v=[a,b]. This vector has two important properties: 1) direction and 2) length.

To understand the direction of v = [a, b], imagine moving a units along the x-axis and then moving b units along the y-axis. The direction is the path from the original to the final point after movement. This leads us to a critical property of vectors: decomposition. We can decompose any vector v=[a,b] into its components along the coordinate axes: v=a*i+b*j, where i and j are the unit vectors along the x-axis and y-axis, respectively. The length of the vector v = [a,b] is sqrt(a^2+b^2) as the coordinate axes are perpendicular to each other. The three-dimensional vector v = [a,b,c] has a length of sqrt(a^2+b^2+c^2). Similar to the length of the n-dimension vector.

One of the most important operations of vectors is the dot product, denoted as v*m. It takes two vectors of the same dimensions and returns a scalar. For example, v = [a1,b1,c1] and m = [a2,b2,c2], the dot product v*m is defined as a1*a2+b1*b2+c1*c2. The geometric interpretation of the dot product relates to the product of the length of v and the length of the projection of m onto v, expressed as v*m = |v|*|m|*cos(theta). We know c^2 = a^2 + b^2 - 2ab*cos(theta) by the law of cosine, where a, b, and c are the sides of a triangle. In the context of vectors, we can denote c = (v-m), a = v, and b=m. By substituting these expressions, we obtain |v-m|^2 = |v|^2+|m|^2-2|v||m|*cos(theta), which can be rewritten as as (v-m)*(v-m) = v*v+m*m -2|v||m|*cos(theta). This further simplifies to v*m = |v||m|*cos(theta).

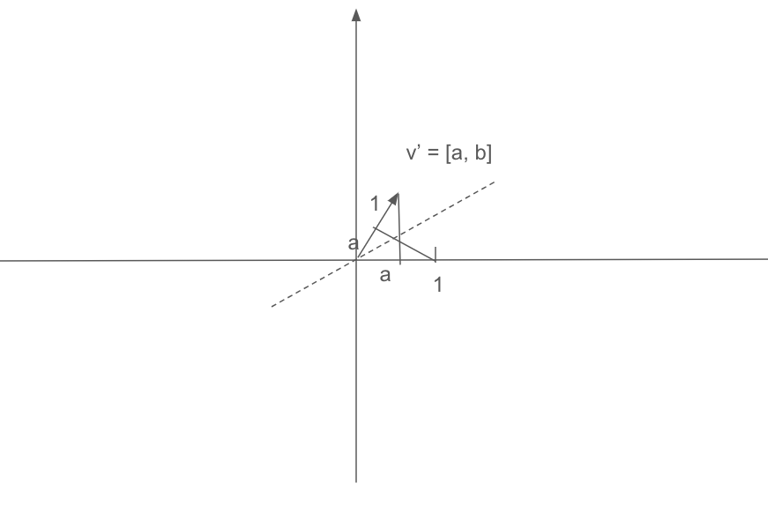
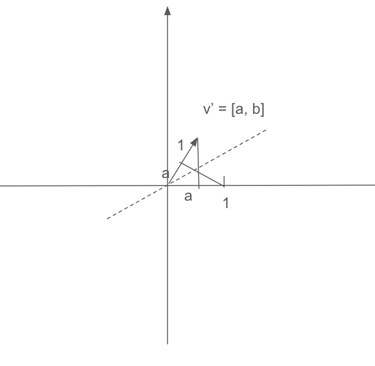
As we can see above, the dot product is a linear function, therefore we can also understand the dot product through duality. The dual of a matrix is the linear transformation it encodes, and the dual of a linear transformation is a certain matrix in that space. In this context, the dot product of v and m can be interpreted as multiplying vector m with matrix v. Here m is a three-dimensional vector and v is a linear transformation after which the original unit vector i, j, k now become a1, b1, c1. Below is a proof for two-dimension space. Consider v' is a unit vector in the direction of V, so V = c*v'. By symmetry, the projection of the original unit vector i onto v' is a, and similarly the projection of unit vector j onto v' is b. Thus v' represents a linear transformation that compresses the original space into the line along v', and m becomes a2*a + b2*b, a point on the line of v'. By scaling v' by c, we obtain V, and m becomes a2*a*c+b2*b*c = a2*a1+b2*b1.

The main applications of the dot product include 1) vector length calculation |v|^2 = v*v, 2) detecting orthogonality, and 3) knowing the angle between two vectors.

Before introducing the concept of the cross-product, let's first revisit the definition of a linear function. A function f is considered linear if it satisfies 1) Homogeneity: f(cx) = cf(x) where c is a constant; 2) Additivity: f(x1+x2) = f(x1)+f(x2). We will introduce cross-product from determinant. For two 2D vectors, the cross product of VxM represents the area of the parallelogram formed by these two vectors, which is the determinant of the matrix [V, M]. For three 3D vectors, we can easily think of the cross-product as the determinant of the 3*3 matrix, which is the volume formed by these three vectors. However, this is not how cross-product is defined for 3D vectors. The cross product of two 3D vectors, VxM, results in another 3D vector P. The vector P has two properties 1) Its length equals the area of the parallelogram formed by V and M; 2) Its direction is perpendicular to the parallelogram following the right-hand rule. To develop an intuitive understanding of the cross-product, let's consider two 3D vectors V and M, along with an input 3D vector A = <x,y,z>. We define a function f that takes A as input and returns the determinant of the matrix M = [A, V, M]. This function f takes a 3D vector as input and outputs a scaler. Moreover, f is a linear function as f(cA) = cf(A) and f(A+B) = f(A+B). Because f is linear, there must exist a vector P such that the product of P and A produce the same output as f(A). The chart below illustrates this.

We can explicitly calculate the dot product on the left hand and the determinant calculation on the right hand to derive the vector P. However, understanding it geometrically is often more intuitive. The determinant represents the volume of the parallelepiped formed by A, V, and M. Geometrically the volume can be thought of as the product of the parallelogram area formed by V and M and the length of the projection of A onto the vector perpendicular to the parallelogram. This is equal to the dot product of P and A, which is the product of the length of P and the length of the projection of A on P. Thus, P is a vector that has the length of the parallelogram area and is perpendicular to the parallelogram.