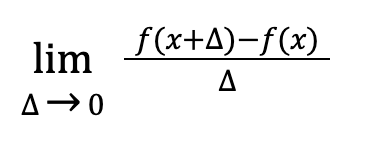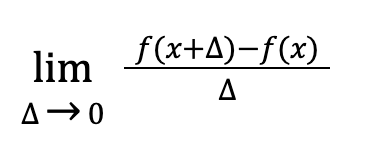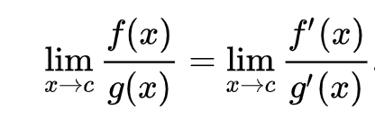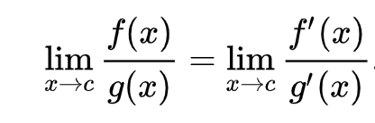The Heart of Derivatives

What is a derivative? Those who have taken a Calculus class might respond with an academic definition or a formula. However, for anyone curious about the concept, a derivative essentially describes how a tiny change in one thing results in a change in another. The ratio between these changes is what we call a derivative. The crucial aspect here is the TINY change, which approaches zero.

People may wonder why this change must approach zero. The reason lies in the nature of derivatives: they represent the best constant approximation for the rate of change at a specific POINT, rather than over an interval. By considering an infinitesimally small change, we can pinpoint the rate of change at that exact point, giving us a more precise understanding of how the function behaves.

Understanding this concept makes it much easier to find the derivative of any function without relying on memorization. For example, the function f(x) = x³. To find its derivative, we should calculate f(x+dx), where dx represents the tiny change. By plugging in this value, we get: f(x+dx) = (x+dx)³ = x³ + 3x²dx + 3x(dx)² + (dx)³. The change in f is f(x+dx) - f(x), which is 3x²dx + 3x(dx)² + (dx)³. The derivative is this change in f divided by the change in x (dx): (3x²dx + 3x(dx)² + (dx)³) / dx = 3x² + 3x(dx) + (dx)². As dx approaches zero, the last two terms become negligible, leaving us with 3x².

Geometry can also help us understand derivatives. Consider the function f(x) = x², which represents the area of a square. If we visualize how the square's area changes as the side increases by dx, we see the increased area is 2x*dx + dx². The derivative is thus 2x + dx, and as dx approaches zero, we're left with 2x. I encourage you to use geometry to find the derivatives of f(x) = 1/x, f(x) = √x, and f(x) = sin(x). This approach can significantly enhance your understanding of derivatives, which is far more valuable than memorizing rules.

While geometry is helpful, it's not always feasible, especially when combining functions. There are three basic ways to combine functions: 1) sum; 2) multiplication; 3) function composition, eg: f(g(x)). Let's explore each:

• Sum: The derivative of the sum of functions is the sum of their individual derivatives. This can be understood through a simple proof or visualization.

• Multiplication: For g(x) = f(x)*t(x), imagine a rectangle with sides f(x) and t(x). The area increase due to a tiny change in x is: f(x)*(t(x+dx) - t(x)) + t(x)*(f(x+dx) - f(x)) + negligible term. The derivative becomes: f(x) * derivative of t(x) + t(x) * derivative of f(x)

• Function Composition: For g(x) = f(t(x)), we apply the chain rule. Let h = t(x). A tiny change in h results in a change in f: dh*derivative of f, where dh = dx*derivative of t. Therefore, dg = derivative of f*derivative of t *dx. The derivative of g is the product of the derivatives of f and t.

Let me present the formal definition of the derivative of f(x) with respect to x. The derivative is essentially a limit.

The L'Hôpital's rule is a useful method for calculating limits when both the numerator and denominator approach zero. Consider the limit lim x->b f(x)/g(x) where both f(x) and g(x) are approaching zero as x approaches b. In such cases, we can compute the limit as lim x->b f'(x)/g'(x). Essentially, we use the ratio of derivates of f(x) and g(x) at the point b to approximate the lim x->b f(x)/g(x). Imagine nudging x by a small amount dx around point b, we have f(b+dx) = f(b)+dx*f'(b) and g(b+dx) = g(b)+dx*g'(b). Thus we can express the original limit as lim f(b)+dx*f'(b)/ g(b)+dx*g'(b) = lim f'(b)/g'(b), given that f(b) and g(b) are zero. L'Hôpital's rule also applies when both f(x) and g(x) are approaching infinity.